🛹 It's How we Roll 🛼
Moment of Inertia 101
💰 Request for Compensation Data 💸
We would be forever grateful if you can fill out this **form** on comp data for us! We’re trying to put together some content on MechE compensation and need more submissions. We will anonymize any submissions (of course), and aggregate data so that it cannot be traced back to you. Whether you’ve only interned or you’re a senior engineer, please help us help you by filling out this form.
⚙️ Mechanical Engineering Resources:
We have put a dozen guides for mechanical engineering students and early professionals on our website
50 Hardware Startups who have raised less than $50 million (perfect internship targets)
How to handle The Behavioral Interview
What it take to be The 10X Intern
💼 Jobs & Internships
For a last minute internship this summer, it is time to turn to local startups. They won’t have job postings, you gotta go knock on doors.
For the fall, lots of exciting internships/co-ops are opening up. Getting these is less competitive than traditional summer internship!
Freshmen - Check out our 4-Year Plan for how to get internships at startups!
Sophomores - Apply To These Positions
AMETEK Mechanical Engineering Intern
General Dynamics Mechanical Engineering Intern
Artivion Product Engineering Intern
Juniors - Full Send Longshots!
Relativity Vehicle Structures Engineering Intern
Saronic Test Engineering Intern
VAST Mechanical Engineering Intern - Electronics Packaging
Seniors & Graduates - It’s Go (Full) Time!
Super Tough:
Anduril Mechanical Engineer - Connected Warfare
Varda Propulsion Development Engineer
Mach Industries Mechanical Engineer
More Reasonable:
Dometic Product Design Engineer
Astrobotic Mechanical Engineer
Abbott Mechanical Engineer
Not seeing what you are looking for? Check out our Job Board for more MechE positions!
👶 Meme Of The Week
🙋♂️ Interview Practice Question of the Week
Lets keep rolling with another technical question!
Company: Tesla
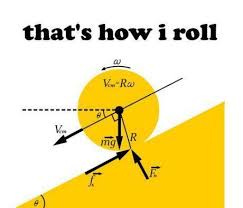
A ring and a disk of equal mass and radius sit at the top of a ramp. When they are released, which one reaches the bottom first? Prove it.
✅ The Answer
This is a great example of a physics fundamentals question. Inertial manipulation is a solution to many of the problems typically asked in interviews, whether it be stress related, or rotational (as in this case).
Governing equation: T = I * alpha
T = torque
Alpha = angular acceleration
I = moment of inertia
Examining each variable in turn, torque is constant. It is equal to force times the distance to the point of rotation (often expressed as T = F * d). In this case, the force is friction, and the distance is the radius. That frictional force remains constant over time due to a constant normal force (for a given angled ramp) and frictional coefficient (Ff = μ * Fn). The main takeaway here is that torque is fixed for a given ramp angle!
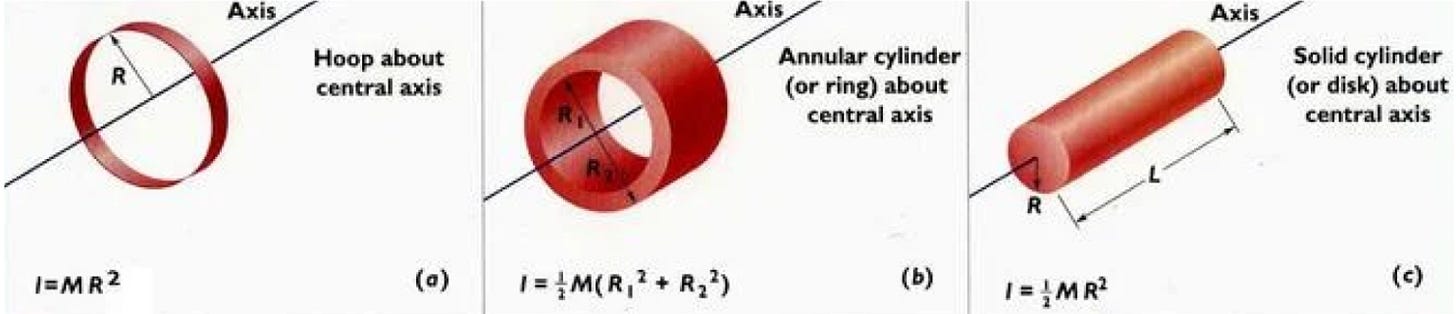
Now, what is inertia? Rotationally, I tend to think of it as how far away from the axis of rotation the mass is concentrated. This is most evident in the fact that the formula for rotational inertia about the center axis of a hoop (think infinitely thin hula hoop), is I = MR2. The formula for a disk on the other hand (think cross section of a hot dog) is I = (1/2) * MR2. This difference is staggering, and means that half the rotational inertia of an object of given mass is lost simply by distributing its weight evenly. This is because it is a squared effect. Simply stated, where I put the mass is more important than how much there is (though obviously, they both play a ~roll~).
If you don’t know the moment of inertia of a disk or ring (think donut or CD shaped - sometimes called an annular cylinder) off the top of your head, don’t worry! As a mechanical engineer trained in first principles, you can just derive it!
In summary:
Inertia of a hoop = M*ro^2
Inertia of a ring = .5M(ro^2 + ri^2)
Inertia of a disk = .5Mro^2
Now we have that torque (constant for both objects) is equal to inertia * angular acceleration. The inertia of a ring is equal to the inertia of a disk, plus the inertia of the smaller removed disk (the donut hole, if you will). That means the inertia of the ring will always be greater than that of an equally massive and sized disk. Higher inertia at constant torque —> lower angular acceleration —> the disk reaches the bottom of the ramp first!
This makes intuitive sense, as inertia in general is how difficult it is to persuade an object to change its motion (qualitatively speaking). Linearly, this tends to be dependent on how massive the object is. A car has greater inertia than a tennis ball, and so a tennis ball hitting you at 60 mph will bounce off and you will have a bruise. Your body, has persuaded the tennis ball to change its motion. If your body tries to convince a car traveling at 60 mph to change its motion, you would have a better chance of success with an emotional appeal (non-inertial) than physical (inertial).
Rotationally then, it makes sense that the more inertia an object has, the harder it will be to rotate. Therefore, at constant radius, the object with less rotational inertia will be easier to rotate and thus reach the bottom first assuming static friction is maintained.